When energy moves from one place to another, it often travels in the form of a wave. This is in contrast with kinetic energy, which is energy an object has BECAUSE it is moving [also, not all moving energy is a wave: a battery can be thrown at someone, and it's stored energy does not suddenly become a wave]. A wave is an oscillation (or pulse) of energy travelling through some medium.

We generally describe two types of waves: transverse and longitudinal. A transverse wave is one in which the medium moves from side to side while the wave moves forward. An example of a transverse wave is an ocean swell: the energy may be moving towards shore, but in general the water molecules are moving up and down. For students who have studied trigonomentry, the sine and cosine waves are transverse.

[A transverse wave.]

In contrast, a longitudinal wave is one in which the pulse moves in the same direction as the medium. A good example of a longitudinal wave is a sound wave. Some source of vibration compresses and rarifies molecules of air, and the pulse moves outward to be heard. The molecules wobble back and forth but do not move overall (to prove this to yourself, remember that even though the speed of sound is about 700 miles per hour, you hardly ever cause a hurricane just by speaking!).
[A longitudinal, or compression wave.]

All waves can be described with the same mathematical tools. The part of a wave have specific names. The high point is called the crest, and the low point is called the trough. The distance between two consecutive crests (or troughs) is called the wavelength. The difference between the highest and lowest points of a wave are called it's amplitude (and can be increased with an amplifier), and a point in space through which a wave passes without causing action is called a node. Finally, an observer watching waves pass by will be able to count the frequency, how many waves pass in a given length of time.

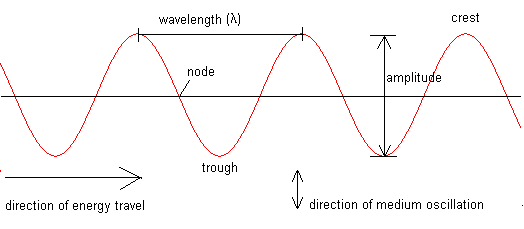
[A labeled transverse wave]

It is relatively easy to picture the descriptions above with with relation to a tranverse wave, but many students have trouble seeing how they can apply to a longitudinal wave like a sound wave. The key is to remember that all our descriptions of waves will be mathematical. In this case, you could graph the density of a longitudinal wave, and the result is a longitudinal wave.

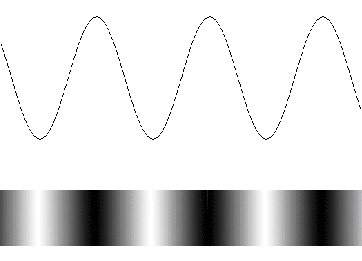
[A transverse and longitudinal wave. Notice that the transverse wave is a graph of ink used in the longitudinal wave.]

THE PART THAT NEEDS TO BE EXPANDED:

In general, we have been discussing sound waves and light waves. Although these two are very different, they have enough similarities and connections with interesting topics that they will both be discussed here. One concept they share is that both waves can be part of a spectrum. A spectrum is a continuous range of values without sudden changes. Visible light waves make up the rainbow, which is only a small part of the electromagnetic spectrum. The electromagnetic spectrum includes "light" with wavelengths far too long for us to see, and light with wavelengths so short that the tear our chemical bonds to bits when we are exposed to them. The audible spectrum is only part of the complete spectrum of sound waves, which includes all the notes we can hear as well as low notes only whales can hear, high ones only bats can hear, earthquake waves, and beyond.

frequency = color <-> pitch
UV <-> ultrasound [PICTURE OF FLOWER BY A BEE; PICTURE OF AN ULTRASOUND BABY]
IR <-> subsonic
Octaves? Chords?
UV, IR, Radio, radar, micro, etc...

wavelength and frequency are inversely related, so speed = wavelength x frequency, which is written as an equation:

c = ln

l is the Greek letter lambda which stands for wavelength, and n is the Greek letter nu which stands for fequency.
The speed of sound is about 330 m/s in air, but it varies greatly depending on temperature and density (including if it's in a rock or water...). The speed of sound msut be known for each specific situation investigated, but fortunatley for you we are not interested in sound here. The speed of light is 300,000,000 m/s (3.0p8) in a vacuum, and it hardly varies at all in most media. This constant is the ultimate speed limit of the universe, and it will always be provided for reference.

Another difference between light and sound is that sound needs medium through which to travel, but light does not. To prove this to yourself, consider that the sun provides enough light and energy to keep life thriving and illuminated on the whole planet, but you never hear the slightest whisper of sound from it!

Energy is directly related to frequency according to the formula E=hn. "h" is Planck's constant, with a value of 6.63n34 J/Hz. This is also a constant that will always be provided.

Photoelectric effect
Energy levels; the effect of # of protons
line spectra [& absorption spectra] & identifying elements.

[light and energy worksheet]
[flame tests]
[etc]

Interesting Links

Possible Spectrum Lab 01
http://imagine.gsfc.nasa.gov/docs/teachers/lessons/supernova/supernova_student.html

Possible Specrtum Lab 02
http://home.earthlink.net/~ssbeaton/labs/atomtheorylabs.html

Really Good Spectrum Lab (with pictures)
http://www.astro.washington.edu/labs/clearinghouse/labs/Spectra/spectra.html

Good Solar Spectrum notes
http://www.astro.uiuc.edu/~kaler/sow/spectra.html

AWESOME line spectrum simulator
http://home.achilles.net/~jtalbot/data/elements/index.html

Shockwave Geisler Tube simulator
http://phys.educ.ksu.edu/vqm/html/absorption.html